A cute "open" problem on polygons
11 Dec 2019Here is a cute problem that appeared on a chat channel of University of Chile a few months ago. To my knowledge this is still open, but as it seems rather natural, the answer is probably known somewhere.
Consider the following transformation: take a polygon in the plane and then dilate it along the $x$-axis.
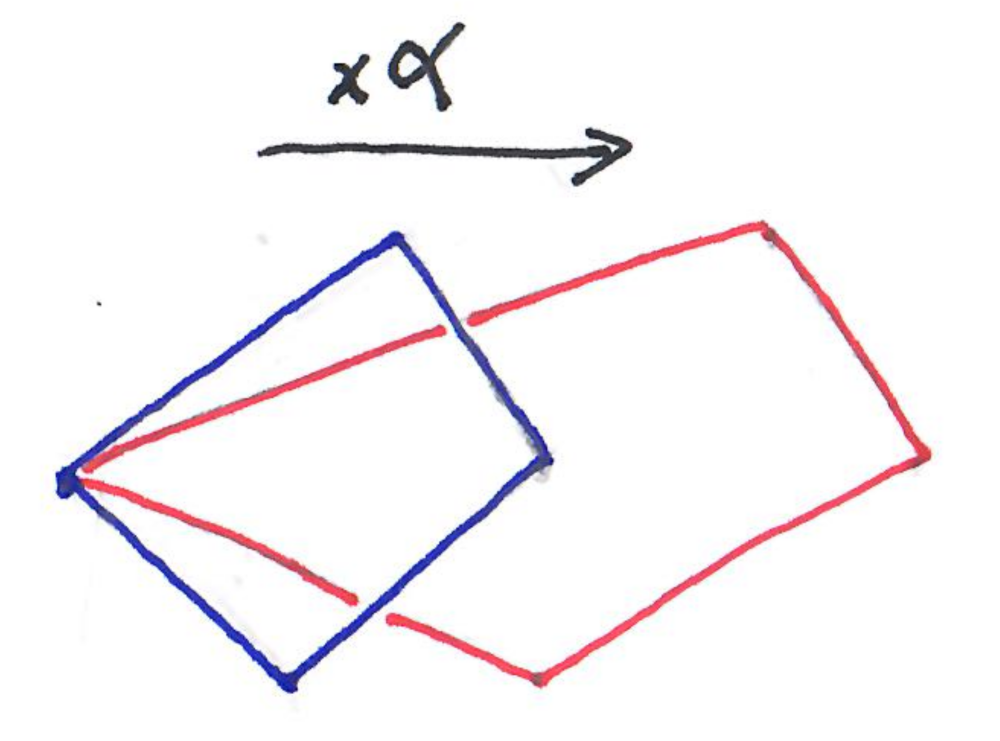
In other words, the $x$ coordinates of the vertices are multiplied by some expansion factor $\alpha$. On the picture the expansion factor is $\alpha=2$.
Now the question is: is it always true that the original polygon fits in the dilated polygon? Note that you are allowed to rotate and translate these as you like.
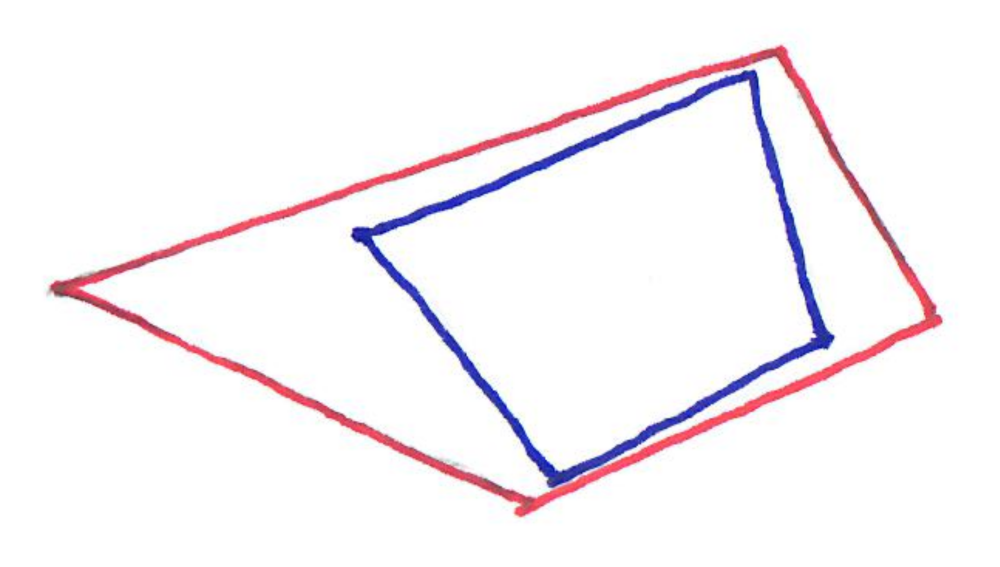
We have thought a bit about this at some point, and we have a proof for triangles, but not much more…